题目描述:
给你一个有 n 个服务器的计算机网络,服务器编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示服务器 ui 和 vi 之间有一条信息线路,在 一秒 内它们之间可以传输 任意 数目的信息。再给你一个长度为 n 且下标从 0 开始的整数数组 patience 。
题目保证所有服务器都是 相通 的,也就是说一个信息从任意服务器出发,都可以通过这些信息线路直接或间接地到达任何其他服务器。
编号为 0 的服务器是 主 服务器,其他服务器为 数据 服务器。每个数据服务器都要向主服务器发送信息,并等待回复。信息在服务器之间按 最优 线路传输,也就是说每个信息都会以 最少时间 到达主服务器。主服务器会处理 所有 新到达的信息并 立即 按照每条信息来时的路线 反方向 发送回复信息。
在 0 秒的开始,所有数据服务器都会发送各自需要处理的信息。从第 1 秒开始,每 一秒最 开始 时,每个数据服务器都会检查它是否收到了主服务器的回复信息(包括新发出信息的回复信息):
- 如果还没收到任何回复信息,那么该服务器会周期性 重发 信息。数据服务器
i 每 patience[i] 秒都会重发一条信息,也就是说,数据服务器 i 在上一次发送信息给主服务器后的 patience[i] 秒 后 会重发一条信息给主服务器。
- 否则,该数据服务器 不会重发 信息。
当没有任何信息在线路上传输或者到达某服务器时,该计算机网络变为 空闲 状态。
请返回计算机网络变为 空闲 状态的 最早秒数 。
示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| 输入:edges = [[0,1],[1,2]], patience = [0,2,1]
输出:8
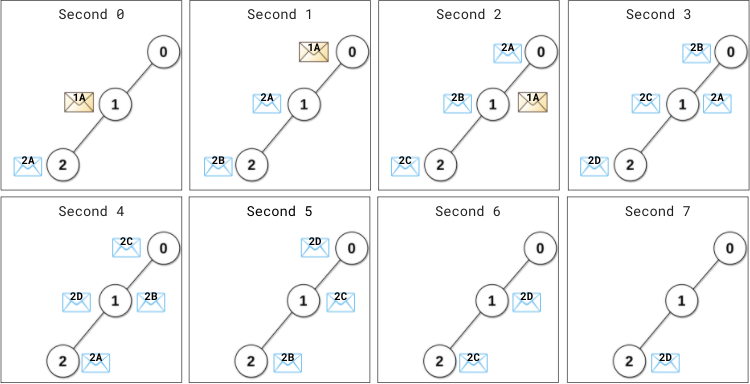
解释:
0 秒最开始时,
- 数据服务器 1 给主服务器发出信息(用 1A 表示)。
- 数据服务器 2 给主服务器发出信息(用 2A 表示)。
1 秒时,
- 信息 1A 到达主服务器,主服务器立刻处理信息 1A 并发出 1A 的回复信息。
- 数据服务器 1 还没收到任何回复。距离上次发出信息过去了 1 秒(1 < patience[1] = 2),所以不会重发信息。
- 数据服务器 2 还没收到任何回复。距离上次发出信息过去了 1 秒(1 == patience[2] = 1),所以它重发一条信息(用 2B 表示)。
2 秒时,
- 回复信息 1A 到达服务器 1 ,服务器 1 不会再重发信息。
- 信息 2A 到达主服务器,主服务器立刻处理信息 2A 并发出 2A 的回复信息。
- 服务器 2 重发一条信息(用 2C 表示)。
...
4 秒时,
- 回复信息 2A 到达服务器 2 ,服务器 2 不会再重发信息。
...
7 秒时,回复信息 2D 到达服务器 2 。
从第 8 秒开始,不再有任何信息在服务器之间传输,也不再有信息到达服务器。
所以第 8 秒是网络变空闲的最早时刻。
|
示例 2:

1
2
3
4
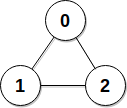
| 输入:edges = [[0,1],[0,2],[1,2]], patience = [0,10,10]
输出:3
解释:数据服务器 1 和 2 第 2 秒初收到回复信息。
从第 3 秒开始,网络变空闲。
|
提示:
n == patience.length2 <= n <= 105patience[0] == 0- 对于
1 <= i < n ,满足 1 <= patience[i] <= 105
1 <= edges.length <= min(105, n * (n - 1) / 2)edges[i].length == 20 <= ui, vi < nui != vi- 不会有重边。
- 每个服务器都直接或间接与别的服务器相连。
思路
这里每个服务器最后变的空闲的时间都是相互独立的,所以我们算出每一个服务器接收最后一条消息的时间然后取最大的那一个就行了。
要计算这个的时间,首先肯定是需要计算每个服务器到服务器0的最短距离,这里刚开始使用的是迪杰斯特拉,但是提交之后超时了,然后观察到所有服务器的距离都是1,所以直接BFS就可以得到距离。
然后考虑怎么计算每个服务器的接受到最后一条消息的时间,接受最后一条消息的时间=发出最后一条消息的时间+2*服务器距离+1,所以最后需要计算的是最后一条消息发出的时间,如果距离距离×2<=发送的间隔时间的话,那么最后一条消息就是第一条消息,否则:
在停止发消息前,经历了2×距离−1的时间,再此期间则会发送⌊patience[i]2×距离−1⌋条消息,那么最后一条消息的时间就是:
⌊patience[i]2×距离−1⌋×patience[i]
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| use std::collections::VecDeque;
impl Solution {
pub fn network_becomes_idle(edges: Vec<Vec<i32>>, patience: Vec<i32>) -> i32 {
let num_point = patience.len();
let mut graph = vec![vec![]; num_point];
edges.iter().for_each(|x| {
graph[x[0] as usize].push(x[1] as usize);
graph[x[1] as usize].push(x[0] as usize);
});
let mut distance = vec![num_point as i32; num_point];
let mut visited = vec![false; num_point];
visited[0] = true;
distance[0] = 0;
let mut queue = VecDeque::new();
queue.push_back(0);
while !queue.is_empty() {
let cur = queue.pop_front().unwrap();
graph[cur].iter().for_each(|&x| {
if !visited[x] {
distance[x] = distance[cur] + 1;
visited[x] = true;
queue.push_back(x);
}
})
}
let mut ans = 0;
for i in 1..num_point {
ans = ans.max(2 * distance[i] + 1 + if distance[i] * 2 <= patience[i] {
0
} else {
(2 * distance[i] - 1) / patience[i] * patience[i]
})
}
ans
}
}
|