Leetcode 2020-04月份每日一题
Xhofe Lv3
  2020-04-01 17:20:18 2020-04-01 17:20      12k 字  57 分钟  

Ya7b0e.png

1-10

01 1111. 有效括号的嵌套深度

题目

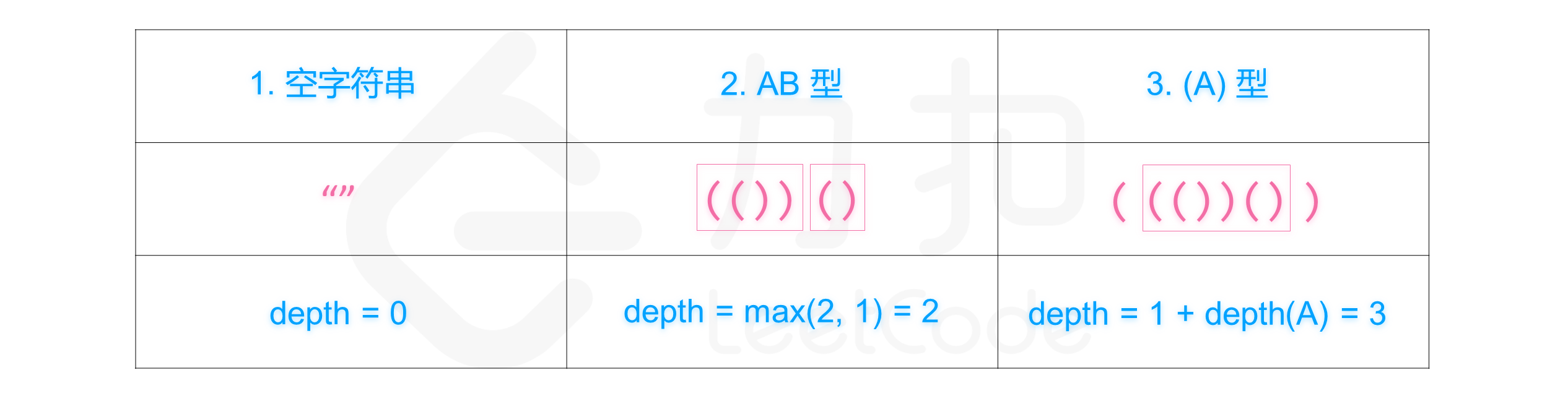
有效括号字符串 定义：对于每个左括号，都能找到与之对应的右括号，反之亦然。详情参见题末「有效括号字符串」部分。

嵌套深度 depth 定义：即有效括号字符串嵌套的层数，depth(A) 表示有效括号字符串 A 的嵌套深度。详情参见题末「嵌套深度」部分。

有效括号字符串类型与对应的嵌套深度计算方法如下图所示：

给你一个「有效括号字符串」 seq，请你将其分成两个不相交的有效括号字符串，A 和 B，并使这两个字符串的深度最小。

  • 不相交：每个 seq[i] 只能分给 A 和 B 二者中的一个，不能既属于 A 也属于 B 。

  • A 或 B 中的元素在原字符串中可以不连续。

  • A.length + B.length = seq.length

  • 深度最小：max(depth(A), depth(B)) 的可能取值最小。

划分方案用一个长度为 seq.length 的答案数组 answer 表示，编码规则如下：

  • answer[i] = 0，seq[i] 分给 A 。
  • answer[i] = 1，seq[i] 分给 B 。

如果存在多个满足要求的答案，只需返回其中任意 一个 即可。

思路

首先的思路是使用栈，先计算出最大深度是多少，然后可知分成两部分的最大深度最大为(depth+1)/2；所以在此使用栈进行记录，每当碰到括号深度大于最大深度时，就分配给另一半。

进阶：题面中的depth其实就是栈的最大深度。“你需要从中选出任意一组有效括号字符串 A 和 B，使 max(depth(A), depth(B)) 的可能取值最小”。这句话其实相当于让A字符串和B字符串的depth尽可能的接近。为什么呢？因为seq对应的栈上，每个左括号都对应一个深度，而这个左括号，要么是A的，要么是B的。所以，栈上的左括号只要按奇偶分配给A和B就可以啦！

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public int[] maxDepthAfterSplit(String seq) {//()(())(((())))((()))()
        int[] res=new int[seq.length()];
        int depth=depthBrackets(seq);
        int maxD=(depth+1)/2;
        Stack<Character> stack=new Stack<>();
        int i=0;
        stack.push(seq.charAt(i));res[i]=0;i++;
        while (i<seq.length()){
            char c=seq.charAt(i);
            if (c=='(')stack.push(c);
            if (stack.size()>maxD){
                res[i]=1;
            }else {
                res[i]=0;
            }
            if (c==')')stack.pop();
            i++;
        }
        return res;
    }
    private int depthBrackets(String seq){
        if (seq.length()==0)return 0;
        Stack<Character> stack=new Stack<>();
        int res=0;
        int i=0;
        stack.push(seq.charAt(i));
        i++;
        while (i<seq.length()){
            res=Math.max(res,stack.size());
            char c=seq.charAt(i);i++;
            if (c=='(')stack.push(c);
            else stack.pop();
        }
        return res;
    }
}
//进阶
class Solution {
    public int[] maxDepthAfterSplit(String seq) {
        int[] ans = new int [seq.length()];
        int idx = 0;
        for(char c: seq.toCharArray()) {
            ans[idx++] = c == '(' ? ((idx + 1) & 1) : idx & 1;
        }
        return ans;
    }
}

02 289. 生命游戏

题目

根据 百度百科 ，生命游戏，简称为生命，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态：1 即为活细胞（live），或 0 即为死细胞（dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

  • 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；

  • 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；

  • 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；

  • 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

根据当前状态，写一个函数来计算面板上所有细胞的下一个（一次更新后的）状态。下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入： 
[
  [0,1,0],
  [0,0,1],
  [1,1,1],
  [0,0,0]
]
输出：
[
  [0,0,0],
  [1,0,1],
  [0,1,1],
  [0,1,0]
]

进阶：

  • 你可以使用原地算法解决本题吗？请注意，面板上所有格子需要同时被更新：你不能先更新某些格子，然后使用它们的更新后的值再更新其他格子。
  • 本题中，我们使用二维数组来表示面板。原则上，面板是无限的，但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题？
思路

本题的主要难度是需要原地解决本题，不能开辟新的数组，如果可以就很简单了。所以主要思路就是利用int可以存储多位的思想，先把下一状态存储在高位上，计算完所有之后，再吧高位上的值更新到地位。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    private int[][] directions=new int[][]{{-1,-1},{0,-1},{-1,0},{0,1},{1,0},{1,1},{-1,1},{1,-1}};
    public void gameOfLife(int[][] board) {
        //int 存储多位
        if (board.length==0||board[0].length==0)return;
        int live;
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                live=0;
                for (int k = 0; k < 8; k++) {
                    int newi=i+directions[k][0];
                    int newj=j+directions[k][1];
                    if (newi>=0&&newi<board.length&&newj>=0&&newj<board[0].length){
                        if ((board[newi][newj]&1)==1)live++;
                    }
                }
                if ((board[i][j]&1)==1){
                    if (live==2||live==3)board[i][j]=3;
                }else {
                    if (live==3)board[i][j]=2;
                }
            }
        }
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                board[i][j]>>=1;
            }
        }
    }
}

03 8. 字符串转换整数 (atoi)

题目

请你来实现一个 atoi函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。接下来的转化规则如下：

  • 如果第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字字符组合起来，形成一个有符号整数。
  • 假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成一个整数。
  • 该字符串在有效的整数部分之后也可能会存在多余的字符，那么这些字符可以被忽略，它们对函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换，即无法进行有效转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0 。

提示：

  • 本题中的空白字符只包括空格字符 ’ ’ 。
  • 假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围，请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。

示例 1:

1
2
输入: "42"
输出: 42

示例 2:

1
2
3
4
输入: "   -42"
输出: -42
解释: 第一个非空白字符为 '-', 它是一个负号。
     我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。
思路

搞人心态的题，直接copy

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    public int myAtoi(String str) {
        int len = str.length();
        // 去除前导空格
        int index = 0;
        while (index < len) {
            if (str.charAt(index) != ' ') {
                break;
            }
            index++;
        }
        if (index == len) {
            return 0;
        }
        // 第 1 个字符如果是符号，判断合法性，并记录正负
        int sign = 1;
        char firstChar = str.charAt(index);
        if (firstChar == '+') {
            index++;
            sign = 1;
        } else if (firstChar == '-') {
            index++;
            sign = -1;
        }
        // 不能使用 long 类型，这是题目说的
        int res = 0;
        while (index < len) {
            char currChar = str.charAt(index);
            // 判断合法性
            if (currChar > '9' || currChar < '0') {
                break;
            }
            // 题目中说：环境只能存储 32 位大小的有符号整数，因此，需要提前判断乘以 10 以后是否越界
            if (res > Integer.MAX_VALUE / 10 || (res == Integer.MAX_VALUE / 10 && (currChar - '0') > Integer.MAX_VALUE % 10)) {
                return Integer.MAX_VALUE;
            }
            if (res < Integer.MIN_VALUE / 10 || (res == Integer.MIN_VALUE / 10 && (currChar - '0') > -(Integer.MIN_VALUE % 10))) {
                return Integer.MIN_VALUE;
            }s
            // 每一步都把符号位乘进去
            res = res * 10 + sign * (currChar - '0');
            index++;
        }

        return res;
    }
}

04 42. 接雨水

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

1
2
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
思路

双指针进行遍历，遍历时分别记录两边的最高的柱子，每遍历到一个柱子，判断它与两端的高度，若比两端的最高的柱子都低，则可以接到雨水，若不是更新最高的柱子。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int trap(int[] height) {
        if (height==null||height.length<2)return 0;
        int len=height.length;
        int left=0,right=len-1;
        int leftmax=0,rightmax=0;
        int res=0;
        while (left<right){
            if (height[left]<height[right]){
                if (height[left]>leftmax)leftmax=height[left];
                else res+=leftmax-height[left];
                left++;
            }else {
                if (height[right]>rightmax)rightmax=height[right];
                else res+=rightmax-height[right];
                right--;
            }
        }
        return res;
    }
}

05 460. LFU缓存

题目

请你为 最不经常使用（LFU）缓存算法设计并实现数据结构。它应该支持以下操作：get 和 put。

  • get(key) - 如果键存在于缓存中，则获取键的值（总是正数），否则返回 -1。
  • put(key, value)- 如果键已存在，则变更其值；如果键不存在，请插入键值对。当缓存达到其容量时，则应该在插入新项之前，使最不经常使用的项无效。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除最久未使用的键。

「项的使用次数」就是自插入该项以来对其调用 get 和 put 函数的次数之和。使用次数会在对应项被移除后置为 0 。

进阶：
你是否可以在 O(1) 时间复杂度内执行两项操作？

示例：

1
2
3
4
5
6
7
8
9
10
11
12
LFUCache cache = new LFUCache( 2 /* capacity (缓存容量) */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回 1
cache.put(3, 3);    // 去除 key 2
cache.get(2);       // 返回 -1 (未找到key 2)
cache.get(3);       // 返回 3
cache.put(4, 4);    // 去除 key 1
cache.get(1);       // 返回 -1 (未找到 key 1)
cache.get(3);       // 返回 3
cache.get(4);       // 返回 4
思路

四个数组分别存储键、值，计数以及最近访问的列表。官方O(1)用的是双哈希表。。。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class LFUCache {
    private int[] keys;
    private int[] values;
    private int[] counts;
    private int[] recents;
    private int now;
    int flag=0;
    public LFUCache(int capacity) {
        keys=new int[capacity];
        values=new int[capacity];
        counts=new int[capacity];
        recents=new int[capacity];
        now=0;
    }

    public int get(int key) {
        for (int i = 0; i < flag; i++) {
            if (key==keys[i]){
                counts[i]++;
                recents[i]=(++now);
                return values[i];
            }
        }return -1;
    }

    public void put(int key, int value) {
        if (keys.length==0)return;
        for (int i = 0; i < flag; i++) {
            if (key==keys[i]){
                counts[i]++;
                values[i]=value;
                recents[i]=now++;
                return;
            }
        }
        if (flag<values.length){
            keys[flag]=key;
            values[flag]=value;
            counts[flag]=1;
            recents[flag]=now++;
            flag++;
        }else {
            List<Integer> list=new ArrayList<>();
            int min=counts[0];
            list.add(0);
            for (int i = 1; i < counts.length; i++) {
                if (counts[i]==min)list.add(i);
                else if (counts[i]<min){
                    min=counts[i];
                    list.clear();
                    list.add(i);
                }
            }
            int index=list.get(0);
            for (int i:list){
                if (recents[i]<recents[index]){
                    index=i;
                }
            }
            keys[index]=key;
            values[index]=value;
            counts[index]=1;
            recents[index]=now++;
        }
    }
}

06 72. 编辑距离

题目

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

  1. 插入一个字符
  2. 删除一个字符
  3. 替换一个字符

示例 1：

1
2
3
4
5
6
输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

1
2
3
4
5
6
7
8
输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
思路

dp,dp[i][j]记录word1前i和word2前j个字符的最短距离，就可以得出转移方程：dp[i+1][j+1]=word1.charAt(i)==word2.charAt(j)?dp[i][j]:Math.min(dp[i][j],Math.min(dp[i][j+1],dp[i+1][j]))+1;dp[i+1][j+1]=word1.charAt(i)==word2.charAt(j)?dp[i][j]:Math.min(dp[i][j],Math.min(dp[i][j+1],dp[i+1][j]))+1;

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int minDistance(String word1, String word2) {
        //dp问题
        int[][] dp=new int[word1.length()+1][word2.length()+1];
        for (int i = 1; i < word1.length()+1; i++) {
            dp[i][0]=i;
        }
        for (int i = 1; i < word2.length()+1; i++) {
            dp[0][i]=i;
        }
        for (int i = 0; i < word1.length(); i++) {
            for (int j = 0; j < word2.length(); j++) {
                dp[i+1][j+1]=word1.charAt(i)==word2.charAt(j)?dp[i][j]:Math.min(dp[i][j],Math.min(dp[i][j+1],dp[i+1][j]))+1;
            }
        }
        return dp[word1.length()][word2.length()];
    }
}

07 面试题 01.07. 旋转矩阵

题目

给你一幅由 N × N 矩阵表示的图像，其中每个像素的大小为 4 字节。请你设计一种算法，将图像旋转 90 度。

不占用额外内存空间能否做到？

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]
思路

就硬旋转，找出每个值对应的位置，四个交换。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public void rotate(int[][] matrix) {
        int len=matrix.length;
        int temp;
        for (int i = 0; i < len/2; i++) {
            for (int j = i; j < len-i-1; j++) {
                temp=matrix[i][j];
                matrix[i][j]=matrix[len-j-1][i];
                matrix[len-j-1][i]=matrix[len-1-i][len-j-1];
                matrix[len-1-i][len-j-1]=matrix[j][len-i-1];
                matrix[j][len-i-1]=temp;
            }
        }
    }
}

08 剑指 Offer 13. 机器人的运动范围

题目

地上有一个m行n列的方格，从坐标 [0,0]到坐标 [m-1,n-1]。一个机器人从坐标[0, 0]的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格[35, 37]，因为3+5+3+7=18。但它不能进入方格[35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：

1
2
输入：m = 2, n = 3, k = 1
输出：3

示例 2：

1
2
输入：m = 3, n = 1, k = 0
输出：1

提示：

  • 1 <= n,m <= 100
  • 0 <= k <= 20
思路

深搜，并记录是否访问即可。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    private boolean[][] visited;
    private int res;
    private int[][]conditions={{-1,0},{1,0},{0,-1},{0,1}};
    public int movingCount(int m, int n, int k) {
        visited=new boolean[m][n];
        res=0;
        help(0,0,m,n,k);
        return res;
    }
    public void help(int i,int j,int m,int n,int k){
        if (i<0||i==m||j<0||j==n||visited[i][j]||sum(i)+sum(j)>k)return;
        res++;
        visited[i][j]=true;
        for (int l = 0; l < 4; l++) {
            help(i+conditions[l][0],j+conditions[l][1],m,n,k);
        }
    }
    public int sum(int i){
        int res=i%10;
        while (i>9){
            i/=10;
            res+=i%10;
        }
        return res;
    }
}

09 22. 括号生成

题目

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例：

1
2
3
4
5
6
7
8
输入：n = 3
输出：[
       "((()))",
       "(()())",
       "(())()",
       "()(())",
       "()()()"
     ]
思路

应该算是回溯吧，但是没有返回的步骤。和深搜类似。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    List<String> generateParenthesisRes;
    public List<String> generateParenthesis(int n) {
        generateParenthesisRes=new ArrayList<>();
        dfs("(",1,0,n);
        return generateParenthesisRes;
    }
    void dfs(String str,int left,int right,int n){
        if (left+right==(n<<1)){ generateParenthesisRes.add(str);return; }
        if (left<n)dfs(str+"(",left+1,right,n);
        if (left>right)dfs(str+")",left,right+1,n);
    }
}

10 151. 翻转字符串里的单词

题目

给定一个字符串，逐个翻转字符串中的每个单词。

示例 1：

1
2
输入: "the sky is blue"
输出: "blue is sky the"

示例 2：

1
2
3
输入: "  hello world!  "
输出: "world! hello"
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

示例 3：

1
2
3
输入: "a good   example"
输出: "example good a"
解释: 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

说明：

  • 无空格字符构成一个单词。
  • 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。
  • 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。
思路

分割字符串，再倒着组装。。

code
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public String reverseWords(String s) {
        StringBuilder res= new StringBuilder();
        String[] arr=s.split(" ");
        for (int i=arr.length-1;i>=0;i--){
            if (arr[i].equals(""))continue;
            res.append(arr[i]).append(" ");
        }
        return res.length()>0?res.substring(0,res.length()-1):res.toString();
    }
}

11-20

11 887. 鸡蛋掉落

题目

你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。

每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。

你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。

每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。

你的目标是确切地知道 F 的值是多少。

无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？

示例 1：

1
2
3
4
5
6
7
输入：K = 1, N = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，我们肯定知道 F = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，我们肯定知道 F = 1 。
如果它没碎，那么我们肯定知道 F = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 F 是多少。

示例 2：

1
2
输入：K = 2, N = 6
输出：3

示例 3：

1
2
输入：K = 3, N = 14
输出：4

提示：

  1. 1 <= K <= 100
  2. 1 <= N <= 10000
思路

dp:dp[k][m]表示k个鸡蛋移动m步可以确定的层数 (忘了在哪看的了。。。)

假设我们有 k 个鸡蛋可以移动 m 步，考虑某一步 t 应该在哪一层丢鸡蛋？一个正确的选择是在 dp[k-1][t-1] + 1层丢鸡蛋，结果分两种情况：

  • 如果鸡蛋碎了，我们首先排除了该层以上的所有楼层（不管这个楼有多高），而对于剩下的dp[k-1][t-1]层楼，我们一定能用 k-1 个鸡蛋在 t-1 步内求解。因此这种情况下，我们总共可以求解无限高的楼层。可见，这是一种非常好的情况，但并不总是发生。
  • 如果鸡蛋没碎，我们首先排除了该层以下的 dp[k-1][t-1]层楼，此时我们还有 k 个蛋和 t-1 步，那么我们去该层以上的楼层继续测得 dp[k][t-1]层楼。因此这种情况下，我们总共可以求解dp[k-1][t-1] + dp[k][t-1] + 1层楼。

得到：

dp[k][m]=dp[k−1][m−1]+dp[k][m−1]+1dp[k][m]=dp[k-1][m-1]+dp[k][m-1]+1

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int superEggDrop(int K, int N) {
        if (K==1||N==0||N==1)return N;
        int[] dp=new int[K+1];
        dp[0]=0;//零个鸡蛋
        for (int i = 1; i < N+1; i++) {//步数
            for (int j = K; j > 0; --j) {//鸡蛋数量
                dp[j]=dp[j-1]+dp[j]+1;
                if (dp[j]>=N)return i;
            }
        }
        return 0;
    }
}

12 面试题 16.03. 交点

题目

给定两条线段（表示为起点start = {X1, Y1}和终点end = {X2, Y2}），如果它们有交点，请计算其交点，没有交点则返回空值。

要求浮点型误差不超过10^-6。若有多个交点（线段重叠）则返回 X 值最小的点，X 坐标相同则返回 Y 值最小的点。

示例 1：

1
2
3
4
输入：
line1 = {0, 0}, {1, 0}
line2 = {1, 1}, {0, -1}
输出： {0.5, 0}

示例 2：

1
2
3
4
输入：
line1 = {0, 0}, {3, 3}
line2 = {1, 1}, {2, 2}
输出： {1, 1}

示例 3：

1
2
3
4
输入：
line1 = {0, 0}, {1, 1}
line2 = {1, 0}, {2, 1}
输出： {}，两条线段没有交点

提示：

  • 坐标绝对值不会超过 2^7
  • 输入的坐标均是有效的二维坐标
思路

搞人的题，copy！！！

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Solution {
    // 判断 (xk, yk) 是否在「线段」(x1, y1)~(x2, y2) 上
    // 这里的前提是 (xk, yk) 一定在「直线」(x1, y1)~(x2, y2) 上
    Boolean inside(int x1, int y1, int x2, int y2, int xk, int yk) {
        // 若与 x 轴平行，只需要判断 x 的部分
        // 若与 y 轴平行，只需要判断 y 的部分
        // 若为普通线段，则都要判断
        return (x1 == x2 || (Math.min(x1, x2) <= xk && xk <= Math.max(x1, x2))) && (y1 == y2 || (Math.min(y1, y2) <= yk && yk <= Math.max(y1, y2)));
    }
    double[] update(double[] ans, double xk, double yk) {
        // 将一个交点与当前 ans 中的结果进行比较
        // 若更优则替换
        if (ans.length==0 ||xk < ans[0] || (xk == ans[0] && yk < ans[1])) {
            if (ans.length==0)ans=new double[2];
            ans[0] = xk;
            ans[1] = yk;
        }
        return ans;
    }
    public double[] intersection(int[] start1, int[] end1, int[] start2, int[] end2) {
        int x1 = start1[0], y1 = start1[1];
        int x2 = end1[0], y2 = end1[1];
        int x3 = start2[0], y3 = start2[1];
        int x4 = end2[0], y4 = end2[1];

        double[] ans=new double[0];
        // 判断 (x1, y1)~(x2, y2) 和 (x3, y3)~(x4, y3) 是否平行
        if ((y4 - y3) * (x2 - x1) == (y2 - y1) * (x4 - x3)) {
            // 若平行，则判断 (x3, y3) 是否在「直线」(x1, y1)~(x2, y2) 上
            if ((y2 - y1) * (x3 - x1) == (y3 - y1) * (x2 - x1)) {
                // 判断 (x3, y3) 是否在「线段」(x1, y1)~(x2, y2) 上
                if (inside(x1, y1, x2, y2, x3, y3)) {
                    ans=update(ans, (double)x3, (double)y3);
                }
                // 判断 (x4, y4) 是否在「线段」(x1, y1)~(x2, y2) 上
                if (inside(x1, y1, x2, y2, x4, y4)) {
                    ans=update(ans, (double)x4, (double)y4);
                }
                // 判断 (x1, y1) 是否在「线段」(x3, y3)~(x4, y4) 上
                if (inside(x3, y3, x4, y4, x1, y1)) {
                    ans=update(ans, (double)x1, (double)y1);
                }
                // 判断 (x2, y2) 是否在「线段」(x3, y3)~(x4, y4) 上
                if (inside(x3, y3, x4, y4, x2, y2)) {
                    ans=update(ans, (double)x2, (double)y2);
                }
            }
            // 在平行时，其余的所有情况都不会有交点
        }
        else {
            // 联立方程得到 t1 和 t2 的值
            double t1 = (double)(x3 * (y4 - y3) + y1 * (x4 - x3) - y3 * (x4 - x3) - x1 * (y4 - y3)) / (double) ((x2 - x1) * (y4 - y3) - (x4 - x3) * (y2 - y1));
            double t2 = (double)(x1 * (y2 - y1) + y3 * (x2 - x1) - y1 * (x2 - x1) - x3 * (y2 - y1)) / (double) ((x4 - x3) * (y2 - y1) - (x2 - x1) * (y4 - y3));
            // 判断 t1 和 t2 是否均在 [0, 1] 之间
            if (t1 >= 0.0 && t1 <= 1.0 && t2 >= 0.0 && t2 <= 1.0) {
                ans = new double[2];
                ans[0] = x1 + t1 * (x2 - x1);
                ans[1] = y1 + t1 * (y2 - y1);
            }
        }
        return ans;
    }
}

13 355. 设计推特

题目

设计一个简化版的推特(Twitter)，可以让用户实现发送推文，关注/取消关注其他用户，能够看见关注人（包括自己）的最近十条推文。你的设计需要支持以下的几个功能：

  1. postTweet(userId, tweetId): 创建一条新的推文
  2. getNewsFeed(userId): 检索最近的十条推文。每个推文都必须是由此用户关注的人或者是用户自己发出的。推文必须按照时间顺序由最近的开始排序。
  3. follow(followerId, followeeId): 关注一个用户
  4. unfollow(followerId, followeeId): 取消关注一个用户

示例:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Twitter twitter = new Twitter();

// 用户1发送了一条新推文 (用户id = 1, 推文id = 5).
twitter.postTweet(1, 5);

// 用户1的获取推文应当返回一个列表，其中包含一个id为5的推文.
twitter.getNewsFeed(1);

// 用户1关注了用户2.
twitter.follow(1, 2);

// 用户2发送了一个新推文 (推文id = 6).
twitter.postTweet(2, 6);

// 用户1的获取推文应当返回一个列表，其中包含两个推文，id分别为 -> [6, 5].
// 推文id6应当在推文id5之前，因为它是在5之后发送的.
twitter.getNewsFeed(1);

// 用户1取消关注了用户2.
twitter.unfollow(1, 2);

// 用户1的获取推文应当返回一个列表，其中包含一个id为5的推文.
// 因为用户1已经不再关注用户2.
twitter.getNewsFeed(1);
思路

创建Tweet链表类用于记录。两个哈希表分别记录用户对应的链表和关注的人。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
//第二种方法
class Twitter {
    class Tweet{
        int id;
        int time=0;
        Tweet next;
        public Tweet(int id, int time){
            this.id=id;
            this.time=time;
            next=null;
        }
    }
    /** Initialize your data structure here. */
    HashMap<Integer, Tweet> map;
    HashMap<Integer, HashSet<Integer>> followees;
    int timeStamp;
    public Twitter() {
        map=new HashMap<Integer, Tweet>();
        followees=new HashMap<Integer, HashSet<Integer>>();
        timeStamp=0;
    }

    /** Compose a new tweet. */
    public void postTweet(int userId, int tweetId) {
        Tweet temp=new Tweet(tweetId, timeStamp++);
        Tweet head=map.get(userId);
        temp.next=head;
        head=temp;
        map.put(userId, head);
    }

    /** Retrieve the 10 most recent tweet ids in the user's news feed. Each item in the news feed must be posted by users who the user followed or by the user herself. Tweets must be ordered from most recent to least recent. */
    public List<Integer> getNewsFeed(int userId) {
        List<Integer> res=new ArrayList<Integer>();
        List<Tweet> tweets=new ArrayList<Tweet>();
        if(map.containsKey(userId)) tweets.add(map.get(userId));
        HashSet<Integer> followeeIds=followees.get(userId);
        if(followeeIds!=null){
            for(Integer followeeId: followeeIds){
                if(map.containsKey(followeeId))
                    tweets.add(map.get(followeeId));
            }
        }
        for(int i=0; i<10; i++){
            int max_index=-1;
            int max=Integer.MIN_VALUE;
            for(int j=0; j<tweets.size(); j++){
                Tweet temp=tweets.get(j);
                if(temp==null) continue;
                if(temp.time>max){
                    max=temp.time;
                    max_index=j;
                }
            }
            if(max_index>=0){
                res.add(tweets.get(max_index).id);
                tweets.set(max_index, tweets.get(max_index).next);
            }
        }
        return res;
    }

    /** Follower follows a followee. If the operation is invalid, it should be a no-op. */
    public void follow(int followerId, int followeeId) {
        if(followerId==followeeId) return;
        HashSet<Integer> followeeIds = followees.computeIfAbsent(followerId, k -> new HashSet<Integer>());
        followeeIds.add(followeeId);
    }

    /** Follower unfollows a followee. If the operation is invalid, it should be a no-op. */
    public void unfollow(int followerId, int followeeId) {
        HashSet<Integer> followeeIds=followees.get(followerId);
        if(followeeIds==null) return;
        followeeIds.remove(followeeId);
    }
}

14 445. 两数相加 II

题目

给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。

你可以假设除了数字 0 之外，这两个数字都不会以零开头。

进阶：

如果输入链表不能修改该如何处理？换句话说，你不能对列表中的节点进行翻转。

示例：

1
2
输入：(7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 8 -> 0 -> 7
思路

转换成list来做。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        if (l1==null)return l2;
        if (l2==null)return l1;
        List<Integer> list1=new ArrayList<>();
        List<Integer> list2=new ArrayList<>();
        while (l1!=null){
            list1.add(l1.val);
            l1=l1.next;
        }
        while (l2!=null){
            list2.add(l2.val);
            l2=l2.next;
        }
        List<Integer> list=new ArrayList<>();
        int i=list1.size()-1,j=list2.size()-1;
        int k=0;
        while (i>=0&&j>=0){
            int tmp=list1.get(i)+list2.get(j)+k;
            list.add(tmp%10);
            k=tmp/10;
            --i;--j;
        }
        while (i>=0){
            int tmp=list1.get(i)+k;
            list.add(tmp%10);
            k=tmp/10;
            --i;
        }
        while (j>=0){
            int tmp=list2.get(j)+k;
            list.add(tmp%10);
            k=tmp/10;
            --j;
        }
        if (k>0)list.add(k);
        k=list.size()-1;
        ListNode head=new ListNode(list.get(k--));
        ListNode tmp=head;
        while (k>=0){
            tmp.next=new ListNode(list.get(k--));
            tmp=tmp.next;
        }
        return head;
    }
}

15 542. 01 矩阵

题目

给定一个由 0 和 1 组成的矩阵，找出每个元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1:
输入:

1
2
3
0 0 0
0 1 0
0 0 0

输出:

1
2
3
0 0 0
0 1 0
0 0 0

示例 2:
输入:

1
2
3
0 0 0
0 1 0
1 1 1

输出:

1
2
3
0 0 0
0 1 0
1 2 1

注意:

  1. 给定矩阵的元素个数不超过 10000。
  2. 给定矩阵中至少有一个元素是 0。
  3. 矩阵中的元素只在四个方向上相邻: 上、下、左、右。
思路

两遍dp，即可。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int[][] updateMatrix(int[][] matrix) {
        int MAX_V=Integer.MAX_VALUE>>1;
        int [][]res=new int[matrix.length][matrix[0].length];
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                res[i][j]=MAX_V;
                if (matrix[i][j]==0)res[i][j]=0;
                else {
                    if (i>0)res[i][j]=Math.min(res[i][j],res[i-1][j]+1);
                    if (j>0)res[i][j]=Math.min(res[i][j],res[i][j-1]+1);
                }
            }
        }
        for (int i = matrix.length-1; i >= 0; --i) {
            for (int j = matrix[0].length-1; j >= 0; --j) {
                if (matrix[i][j]!=0){
                    if (i<matrix.length-1)res[i][j]=Math.min(res[i][j],res[i+1][j]+1);
                    if (j<matrix[0].length-1)res[i][j]=Math.min(res[i][j],res[i][j+1]+1);
                }
            }
        }
        return res;
    }
}

16 56. 合并区间

题目

给出一个区间的集合，请合并所有重叠的区间。

示例 1:

1
2
3
输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:

1
2
3
输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
思路

贪心，但是比较慢。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals == null || intervals.length == 0 || intervals[0].length == 0) return intervals;
        // 贪心
        Arrays.sort(intervals, Comparator.comparingInt(n -> n[0]));
        List<int[]> list = new LinkedList<>();
        int left = intervals[0][0], right = intervals[0][1];
        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] > right) {
                list.add(new int[]{left, right});
                left = intervals[i][0];
            }
            right = Math.max(right,intervals[i][1]);
        }
        list.add(new int[]{left, right});
        return list.toArray(new int[][]{});
    }
}

17 55. 跳跃游戏

题目

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

1
2
3
输入: [2,3,1,1,4]
输出: true
解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

示例 2:

1
2
3
输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。
思路

从后往前贪心。

code
1
2
3
4
5
6
7
8
9
10
class Solution {
    public boolean canJump(int[] nums) {
        //从后往前贪心
        int index=nums.length-1;
        for (int i = nums.length-2; i >= 0 ; --i) {
            if (index-i<=nums[i])index=i;
        }
        return index==0;
    }
}

18 11. 盛最多水的容器

题目

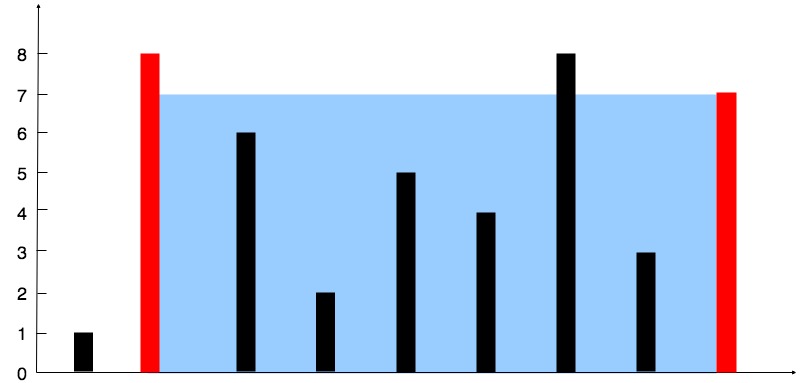
给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

**说明：**你不能倾斜容器，且 n 的值至少为 2。

图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例：

1
2
输入：[1,8,6,2,5,4,8,3,7]
输出：49
思路

双指针，记录两边最高值。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int maxArea(int[] height) {
        if (height == null || height.length == 0) return 0;

        int l = 0, r = height.length - 1, water = 0;
        while (l < r) {
            if (height[l] <= height[r]) {
                int minH = height[l];
                water = Math.max(water, (r - l) * minH);
                while (l < r && height[l] <= minH) l++;
            } else {
                int minH = height[r];
                water = Math.max(water, (r - l) * minH);
                while (l < r && height[r] <= minH) r--;
            }
        }
        return water;
    }
}

19 466. 统计重复个数

题目

由 n 个连接的字符串 s 组成字符串 S，记作 S = [s,n]。例如，["abc",3]=“abcabcabc”。

如果我们可以从 s2 中删除某些字符使其变为 s1，则称字符串 s1 可以从字符串 s2 获得。例如，根据定义，“abc” 可以从 “abdbec” 获得，但不能从 “acbbe” 获得。

现在给你两个非空字符串 s1 和 s2（每个最多 100 个字符长）和两个整数 0 ≤ n1 ≤ 106 和 1 ≤ n2 ≤ 106。现在考虑字符串 S1 和 S2，其中 S1=[s1,n1] 、S2=[s2,n2] 。

请你找出一个可以满足使[S2,M] 从 S1 获得的最大整数 M 。

示例：

1
2
3
4
5
6
输入：
s1 ="acb",n1 = 4
s2 ="ab",n2 = 2

返回：
2
思路

见注释。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public int getMaxRepetitions(String s1, int n1, String s2, int n2) {
                if(s1.length() ==0 || s2.length()==0 || n1==0 || n2 ==0) return 0;
        char[] s1Chars = s1.toCharArray();
        char[] s2Chars = s2.toCharArray();
        int count = 0;
        int index = 0;
        //存储在每个s1字符串中可以匹配出的s2字符串的索引
       int[] indexr = new int[s2Chars.length+1];
        //存储在每个s1字符串时匹配出的s2字符串的个数，可能是包含了前面一个s1循环节的部分
        int[] countr = new int[s2Chars.length+1];
        for(int i=0;i<n1;i++){
            for (char s1Char : s1Chars) {
                if (s1Char == s2Chars[index]) {
                    if (index == s2Chars.length - 1) {
                        count++;
                        index = 0;
                    } else {
                        index++;
                    }
                }
            }
            countr[i] = count;
           indexr[i] = index;
            //剪枝，跳出循环的判断
            //从计数的数组里面去找是否已经出现过该索引。
            //意味着已经出现重复的循环节了。就可以直接计算了。
           for (int k = 0; k < i && indexr[k] == index; k++) {
               int prev_count = countr[k];
               int pattern_count = ((n1 - 1 - k) / (i - k))*(countr[i] - countr[k]);
               int remain_count = countr[k + (n1 - 1 - k) % (i - k)] - countr[k];
               return (prev_count + pattern_count + remain_count) / n2;
           }
        }
        return countr[n1 - 1] / n2;
    }
}

20 200. 岛屿数量

题目

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1:

1
2
3
4
5
6
输入:
11110
11010
11000
00000
输出: 1

示例 2:

1
2
3
4
5
6
7
输入:
11000
11000
00100
00011
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
思路

深搜。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    //dfs
    private int[][] conditions={{0,1},{0,-1},{1,0},{-1,0}};
    public int numIslands(char[][] grid) {
        if (grid==null||grid.length==0||grid[0].length==0)return 0;
        int res=0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (grid[i][j]=='1'){
                    ++res;
                    numIslands(grid,i,j);
                }
            }
        }
        return res;
    }
    public void numIslands(char[][] grid,int i,int j){
        if (i<0||i>=grid.length||j<0||j>=grid[0].length||grid[i][j]!='1')return;
        grid[i][j]='0';
        for (int[] condition : conditions) {
            numIslands(grid, i + condition[0], j + condition[1]);
        }
    }
}

21-30

21 1248. 统计「优美子数组」

题目

给你一个整数数组 nums 和一个整数 k。

如果某个 连续 子数组中恰好有 k 个奇数数字，我们就认为这个子数组是「优美子数组」。

请返回这个数组中「优美子数组」的数目。

示例 1：

1
2
3
输入：nums = [1,1,2,1,1], k = 3
输出：2
解释：包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。

示例 2：

1
2
3
输入：nums = [2,4,6], k = 1
输出：0
解释：数列中不包含任何奇数，所以不存在优美子数组。

示例 3：

1
2
输入：nums = [2,2,2,1,2,2,1,2,2,2], k = 2
输出：16

提示：

  • 1 <= nums.length <= 50000
  • 1 <= nums[i] <= 10^5
  • 1 <= k <= nums.length
思路

双指针~

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int numberOfSubarrays(int[] nums, int k) {
        int res=0,count=0;
        int left=0,right=0;
        int tmp=0;
        while (right<nums.length){
            if (count<k){
                count+=nums[right]&1;
                right++;
            }
            if (count==k){
                tmp=0;
                while (count==k){
                    ++res;++tmp;
                    count-=nums[left]&1;
                    ++left;
                }
            }else res+=tmp;
        }
        return res;
    }
}

22 199. 二叉树的右视图

题目

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例:

1
2
3
4
5
6
7
8
9
输入: [1,2,3,null,5,null,4]
输出: [1, 3, 4]
解释:

   1            <---
 /   \
2     3         <---
 \     \
  5     4       <---
思路

从右向左层级bfs，每次记录第一个。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> res=new LinkedList<>();
        if (root==null)return res;
        Queue<TreeNode> queue=new LinkedList<>();
        queue.add(root);
        TreeNode tmp;
        while (!queue.isEmpty()){
            tmp=queue.poll();
            int len=queue.size();
            res.add(tmp.val);
            if (tmp.right!=null){
                queue.add(tmp.right);
            }
            if (tmp.left!=null){
                queue.add(tmp.left);
            }
            for (int i = 0; i < len; i++) {
                tmp=queue.poll();
                if (tmp.right!=null){
                    queue.add(tmp.right);
                }
                if (tmp.left!=null){
                    queue.add(tmp.left);
                }
            }
        }
        return res;
    }
}

23 面试题 08.11. 硬币

题目

硬币。给定数量不限的硬币，币值为25分、10分、5分和1分，编写代码计算n分有几种表示法。(结果可能会很大，你需要将结果模上1000000007)

示例1:

1
2
3
4
5
 输入: n = 5
 输出：2
 解释: 有两种方式可以凑成总金额:
5=5
5=1+1+1+1+1

示例2:

1
2
3
4
5
6
7
 输入: n = 10
 输出：4
 解释: 有四种方式可以凑成总金额:
10=10
10=5+5
10=5+1+1+1+1+1
10=1+1+1+1+1+1+1+1+1+1

说明：

注意:

你可以假设：

  • 0 <= n (总金额) <= 1000000
思路

动态规划，还有一种数学方法更快。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int waysToChange(int n) {
        //动态规划
        int[] dp=new int[n+1];
        dp[0]=1;
        int[] coins={1,5,10,25};
        for (int i = 0; i < 4; i++) {
            for (int j = coins[i]; j < n + 1; j++) {
                dp[j]=(dp[j]+dp[j-coins[i]])%1000000007;
            }
        }
        return dp[n];
    }
    public int waysToChange(int n) {
        //数学法
        int ans = 0,mod=1000000007;
        for (int i = 0; i * 25 <= n; ++i) {
            int rest = n - i * 25;
            int a = rest / 10;
            int b = rest % 10 / 5;
            ans = (int) ((ans + (long)(a + 1) * (a + b + 1) % mod) % mod);
        }
        return ans;
    }
}

24 剑指 Offer 51. 数组中的逆序对

题目

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

1
2
输入: [7,5,6,4]
输出: 5

限制：

0 <= 数组长度 <= 50000

思路

归并排序一下，就可以得到答案。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    private int res;
    public int reversePairs(int[] nums) {
        res=0;
        mergeSort(nums,0,nums.length-1);
        return res;
    }
    public void mergeSort(int[] arr,int left,int right){
        if (left>=right)return;
        int mid=(left+right)>>1;
        mergeSort(arr,left,mid);
        mergeSort(arr,mid+1,right);
        int[] tmp=new int[right-left+1];
        int index=0,index1=left,index2=mid+1;
        while (index1<=mid&&index2<=right){
            if (arr[index1]<=arr[index2]){
                tmp[index++]=arr[index1++];
            }else {
                tmp[index++]=arr[index2++];
                res+=(mid-index1+1);
            }
        }
        while (index1<=mid)tmp[index++]=arr[index1++];
        while (index2<=right)tmp[index++]=arr[index2++];
        System.arraycopy(tmp, 0, arr, left, tmp.length);
    }
}

25 46. 全排列

题目

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

1
2
3
4
5
6
7
8
9
10
输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]
思路

回溯法~

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        //回溯
        List<List<Integer>> res = new LinkedList<>();
        int[] visited = new int[nums.length];
        backtrack(res, nums, new ArrayList<Integer>(), visited);
        return res;

    }
    private void backtrack(List<List<Integer>> res, int[] nums, ArrayList<Integer> tmp, int[] visited) {
        if (tmp.size() == nums.length) {
            res.add(new ArrayList<>(tmp));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (visited[i] == 1) continue;
            visited[i] = 1;
            tmp.add(nums[i]);
            backtrack(res, nums, tmp, visited);
            visited[i] = 0;
            tmp.remove(tmp.size() - 1);
        }
    }
}

26 23. 合并K个排序链表

题目

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

1
2
3
4
5
6
7
输入:
[
  1->4->5,
  1->3->4,
  2->6
]
输出: 1->1->2->3->4->4->5->6
思路

递归两两合并。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
                int len=lists.length;
        if(lists==null || len==0)return null;
        return fz(lists,0,len-1);
    }
    public ListNode fz(ListNode[] lists,int j,int k){
        if(j>=k)return lists[j];
        int mid=(k-j)/2+j;
        ListNode l1=fz(lists,j,mid);
        ListNode l2=fz(lists,mid+1,k);
        return merge2Lists(l1,l2);
    }
    public ListNode merge2Lists(ListNode l1,ListNode l2){
        if(l1==null)return l2;
        if(l2==null)return l1;
        ListNode p1=l1,p2=l2;
        ListNode current=new ListNode(0);
        ListNode first=current;
        while (p1!=null&&p2!=null){
            if(p1.val<=p2.val){
                current.next=p1;
                p1=p1.next;
                current=current.next;
            }
            else {
                current.next=p2;
                p2=p2.next;
                current=current.next;
            }
        }
        ListNode p=(p1!=null)? p1:p2;
        while (p!=null){
            current.next=p;
            p=p.next;
            current=current.next;
        }
        return first.next;
    }
}

27 33. 搜索旋转排序数组

题目

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

1
2
输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

示例 2:

1
2
输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1
思路

先找出旋转的位置，然后用这个位置一一对应进行二分查找。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int search(int[] nums, int target) {
        int len=nums.length;
        if (len==0)return -1;
        int left=0,right=len-1;
        while (left<right){
            int middle=((right-left)>>1)+left;
            if (nums[right]>nums[middle])right=middle;
            else if (nums[right]<nums[middle])left=middle+1;
            else --right;
        }
        int L=0,R=len-1;
        while (L<R){
            int mid=(R+L)>>1;
            int midIndex=(mid+left)%len;
            if (nums[midIndex]==target)return midIndex;
            else if (nums[midIndex]<target)L=mid+1;
            else R=mid-1;
        }
        if (nums[(L+left)%len]==target)return (L+left)%len;
        return -1;
    }
}

28 剑指 Offer 56 - I. 数组中数字出现的次数

题目

一个整型数组 nums 里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n)，空间复杂度是O(1)。

示例 1：

1
2
输入：nums = [4,1,4,6]
输出：[1,6] 或 [6,1]

示例 2：

1
2
输入：nums = [1,2,10,4,1,4,3,3]
输出：[2,10] 或 [10,2]

限制：

  • 2 <= nums.length <= 10000
思路

主要使用异或运算，再将数组分为两组进行异或。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int[] singleNumbers(int[] nums) {
        // 只计算一组
        int[] res=new int[2];
        int t=0;
        for (int i:nums){
            t^=i;
        }
        int tt=t;
        t=t&(-t);
        for (int i:nums){
            if ((i&t)==0){
                res[0]^=i;
            }
        }
        res[1]=res[0]^tt;
        return res;
    }
}

29 1095. 山脉数组中查找目标值

题目

（这是一个 交互式问题 ）

给你一个 山脉数组 mountainArr，请你返回能够使得 mountainArr.get(index) 等于 target 最小 的下标 index 值。

如果不存在这样的下标 index，就请返回 -1。

何为山脉数组？如果数组 A 是一个山脉数组的话，那它满足如下条件：

首先，A.length >= 3

其次，在 0 < i < A.length - 1 条件下，存在 i 使得：

  • A[0] < A[1] < ... A[i-1] < A[i]
  • A[i] > A[i+1] > ... > A[A.length - 1]

你将 不能直接访问该山脉数组，必须通过 MountainArray 接口来获取数据：

  • MountainArray.get(k) - 会返回数组中索引为k 的元素（下标从 0 开始）
  • MountainArray.length() - 会返回该数组的长度

注意：

对 MountainArray.get 发起超过 100 次调用的提交将被视为错误答案。此外，任何试图规避判题系统的解决方案都将会导致比赛资格被取消。

为了帮助大家更好地理解交互式问题，我们准备了一个样例 “答案”：https://leetcode-cn.com/playground/RKhe3ave，请注意这 不是一个正确答案。

示例 1：

1
2
3
输入：array = [1,2,3,4,5,3,1], target = 3
输出：2
解释：3 在数组中出现了两次，下标分别为 2 和 5，我们返回最小的下标 2。

示例 2：

1
2
3
输入：array = [0,1,2,4,2,1], target = 3
输出：-1
解释：3 在数组中没有出现，返回 -1。

提示：

  • 3 <= mountain_arr.length() <= 10000
  • 0 <= target <= 10^9
  • 0 <= mountain_arr.get(index) <= 10^9
思路

主要的思路就是二分查找，先使用二分法找到数组的峰值。然后左右寻找。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/**
 * // This is MountainArray's API interface.
 * // You should not implement it, or speculate about its implementation
 * interface MountainArray {
 *     public int get(int index) {}
 *     public int length() {}
 * }
 */
 
class Solution {
    private int findInMountainArrayRes=-1;
    public int findInMountainArray(int target, MountainArray mountainArr) {
        if(target==450002)return -1;
        int len=mountainArr.length();
        if (len<50){
            for (int i = 0; i < len; i++) {
                if (mountainArr.get(i)==target)return i;
            }
            return -1;
        }
        int left=0,right=len-1;
        findInMountainArray(target,mountainArr,left,right);
        return findInMountainArrayRes;
    }
    public void findInMountainArray(int target, MountainArray mountainArr,int left,int right) {
        if (right-left<3){
            for (int i = 0; i < 3; i++) {
                if (mountainArr.get(left+i)==target)findInMountainArrayRes(left+i);
            }
            return;
        }
        int middle=(left+right)>>1;
        int mid=mountainArr.get(middle);
        int midL=mountainArr.get(middle-1),midR=mountainArr.get(middle+1);
        if (mid==target){
            findInMountainArrayRes(middle);
            if (mid>midL)return;
        }
        if (mid>midL){
            findInMountainArrayRes(findInMountainArray(target,mountainArr,left,middle-1,true));
            if (findInMountainArrayRes!=-1)return;
        }
        else findInMountainArray(target,mountainArr,left,middle-1);
        if (mid>midR)findInMountainArrayRes(findInMountainArray(target,mountainArr,middle+1,right,false));
        else findInMountainArray(target,mountainArr,middle+1,right);
    }
    public void findInMountainArrayRes(int res){
        if (res==-1)return;
        if (findInMountainArrayRes==-1)findInMountainArrayRes=res;
        else findInMountainArrayRes=Math.min(findInMountainArrayRes,res);
    }
    public int findInMountainArray(int target, MountainArray mountainArr,int left,int right,boolean up) {
        if (left>right)return -1;
        int middle=(left+right)>>1;
        int mid=mountainArr.get(middle);
        if (mid==target)return middle;
        if (left==right)return -1;
        if ((mid>target&&up)||(mid<target&&!up))return findInMountainArray(target,mountainArr,left,middle-1,up);
        return findInMountainArray(target,mountainArr,middle+1,right,up);
    }
}

30 202. 快乐数

题目

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和，然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。如果 可以变为 1，那么这个数就是快乐数。

如果 n 是快乐数就返回 True ；不是，则返回 False 。

示例：

1
2
3
4
5
6
7
输入：19
输出：true
解释：
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1
思路

首先的思路肯定是哈希集合，一直运算发现就返回，否则一直运算到出现重复值。

然后是不快乐的都会进入4的循环，所以判断出现4或1就行了。

code
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public boolean isHappy(int n) {
        while(n!=1&&n!=4){
            int sum=0;
            while(n>0){
                sum += (n%10)*(n%10);
                n /=10;
            }
            n=sum;
        }
        return n==1;
    }
}
  • 本文标题：Leetcode 2020-04月份每日一题
  • 本文作者：Xhofe
  • 创建时间：2020-04-01 17:20:18
  • 本文链接：https://nn.ci/posts/20-04-leetcode.html
  • 版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
 评论