使用队列实现栈的下列操作:
push(x) – 元素 x 入栈
pop() – 移除栈顶元素
top() – 获取栈顶元素
empty() – 返回栈是否为空
你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。 你可以使用 list 或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
你可以假设所有操作都是有效的(例如, 对一个空的栈不会调用 pop 或者 top 操作)。
没啥好说的,就是一个队列存数据,一个队列辅助入栈,入栈时交换两个队列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class MyStack { private Queue<Integer> queue1,queue2; public MyStack () { queue1=new ArrayDeque <>(); queue2=new ArrayDeque <>(); } public void push (int x) { queue1.add(x); while (!queue2.isEmpty())queue1.add(queue2.poll()); Queue tmp=queue1;queue1=queue2;queue2=tmp; } public int pop () { return queue2.poll(); } public int top () { return queue2.peek(); } public boolean empty () { return queue2.isEmpty(); } }
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
进阶:
老题目了,上数据结构的时候就说过,遍历链表,遍历到结点链接到上一个节点并记录该结点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public ListNode reverseList (ListNode head) { if (head==null ||head.next==null )return head; ListNode last=null ; ListNode cur=head; ListNode next=null ; while (cur!=null ){ next=cur.next; cur.next=last; last=cur; cur=next; } return last; } }
给定两个排序后的数组 A 和 B,其中 A 的末端有足够的缓冲空间容纳 B。 编写一个方法,将 B 合并入 A 并排序。
初始化 A 和 B 的元素数量分别为 m 和 n。
示例:
输入:
输出: [1,2,2,3,5,6]
说明:
A.length == n + m
双指针。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public void merge (int [] A, int m, int [] B, int n) { int i=A.length-1 ; m-=1 ;n-=1 ; while (m>=0 &&n>=0 ){ if (A[m]>B[n]){ A[i--]=A[m];m--; }else { A[i--]=B[n];n--; } } while (n>=0 ){ A[i--]=B[n];n--; } } }
在给定的网格中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
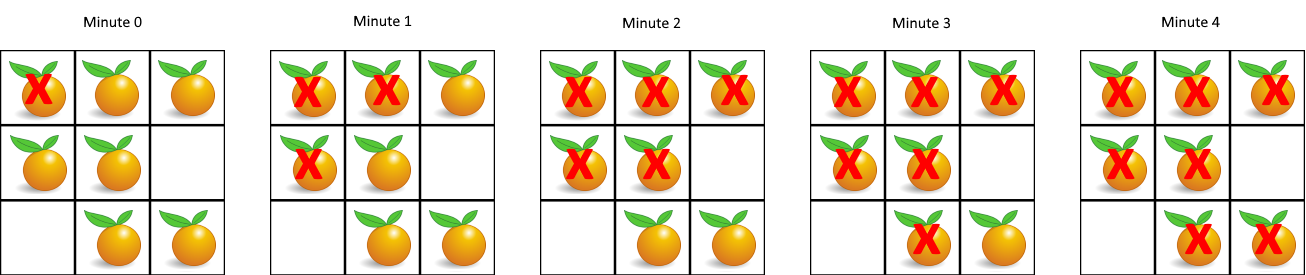
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
示例 1:
1 2 输入:[[2,1,1],[1,1,0],[0,1,1]] 输出:4
示例 2:
1 2 3 输入:[[2,1,1],[0,1,1],[1,0,1]] 输出:-1 解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。
示例 3:
1 2 3 输入:[[0,2]] 输出:0 解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
1 <= grid.length <= 101 <= grid[0].length <= 10grid[i][j] 仅为 0、1 或 2
模拟一遍这个过程,但是每次烂掉的橘子记为-1,之后再统一标记为2,避免一次中的腐烂传播。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class Solution { public int orangesRotting (int [][] grid) { int count = 0 ; while (lan(grid)){ count++; } for (int [] ints : grid) { for (int j = 0 ; j < grid[0 ].length; j++) { if (ints[j] == 1 ) { return -1 ; } } } return count; } public static boolean lan (int [][] grid) { boolean lan=false ; for (int i=0 ;i<=grid.length-1 ;i++){ for (int j = 0 ; j < grid[0 ].length; j++) { if (grid[i][j]==2 ){ if (i-1 >=0 &&grid[i-1 ][j]==1 ){ grid[i-1 ][j]=-1 ; lan=true ; } if (i+1 <grid.length&&grid[i+1 ][j]==1 ){ grid[i+1 ][j]=-1 ; lan=true ; } if (j-1 >=0 &&grid[i][j-1 ]==1 ){ grid[i][j-1 ]=-1 ; lan=true ; } if (j+1 <grid[0 ].length&&grid[i][j+1 ]==1 ){ grid[i][j+1 ]=-1 ; lan=true ; } } } } for (int i=0 ;i<=grid.length-1 ;i++){ for (int j = 0 ; j < grid[0 ].length; j++) { if (grid[i][j]==-1 ){ grid[i][j]=2 ; } } } return lan; } }
排排坐,分糖果。
我们买了一些糖果 candies,打算把它们分给排好队的 n = num_people个小朋友。
给第一个小朋友 1 颗糖果,第二个小朋友 2 颗,依此类推,直到给最后一个小朋友 n 颗糖果。
然后,我们再回到队伍的起点,给第一个小朋友 n + 1 颗糖果,第二个小朋友 n + 2 颗,依此类推,直到给最后一个小朋友 2 * n 颗糖果。
重复上述过程(每次都比上一次多给出一颗糖果,当到达队伍终点后再次从队伍起点开始),直到我们分完所有的糖果。注意,就算我们手中的剩下糖果数不够(不比前一次发出的糖果多),这些糖果也会全部发给当前的小朋友。
返回一个长度为 num_people、元素之和为 candies 的数组,以表示糖果的最终分发情况(即 ans[i] 表示第i 个小朋友分到的糖果数)。
示例 1:
1 2 3 4 5 6 7 输入:candies = 7, num_people = 4 输出:[1,2,3,1] 解释: 第一次,ans[0] += 1,数组变为 [1,0,0,0]。 第二次,ans[1] += 2,数组变为 [1,2,0,0]。 第三次,ans[2] += 3,数组变为 [1,2,3,0]。 第四次,ans[3] += 1(因为此时只剩下 1 颗糖果),最终数组变为 [1,2,3,1]。
示例 2:
1 2 3 4 5 6 7 输入:candies = 10, num_people = 3 输出:[5,2,3] 解释: 第一次,ans[0] += 1,数组变为 [1,0,0]。 第二次,ans[1] += 2,数组变为 [1,2,0]。 第三次,ans[2] += 3,数组变为 [1,2,3]。 第四次,ans[0] += 4,最终数组变为 [5,2,3]。
提示:
1 <= candies <= 10^91 <= num_people <= 1000
纯数学计算,先计算出把所有小朋友发全可以发多少次,然后剩下的糖果模拟发完为止。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution { public int [] distributeCandies(int candies, int num_people) { int [] res=new int [num_people]; int tmp=candies; int count=-1 ; while (tmp>0 ){ candies=tmp;++count; tmp-=num_people*((2 *count+1 )*num_people+1 )/2 ; } for (int i = 0 ; i < num_people; i++) { res[i]=count*(2 *(i+1 )+(count-1 )*num_people)/2 ; tmp=count*num_people+i+1 ; if (candies<=0 )continue ; if (candies>=tmp){ res[i]+=tmp; candies-=tmp; }else { res[i]+=candies; candies=0 ; } } return res; } }
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
示例 1:
输入:target = 9
示例 2:
输入:target = 15
限制:
滑动窗口,因为都是正数,要往目标和靠近,小的时候右边界右移,大的时候左边界右移。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution : def findContinuousSequence (self, target: int ) -> List [List [int ]]: i = 1 j = 1 sum = 0 res = [] while i <= target // 2 : if sum < target: sum += j j += 1 elif sum > target: sum -= i i += 1 else : arr = list (range (i, j)) res.append(arr) sum -= i i += 1 return res
请定义一个队列并实现函数max_value得到队列里的最大值,要求函数max_value、push_back 和 pop_front的均摊时间复杂度都是O(1)。
若队列为空,pop_front和 max_value需要返回 -1
示例 1:
输入 :MaxQueue",“push_back”,“push_back”,“max_value”,“pop_front”,“max_value”]输出 : [null,null,null,2,1,2]
示例 2:
输入 :MaxQueue",“pop_front”,“max_value”]输出 : [null,-1,-1]
限制:
1 <= push_back,pop_front,max_value的总操作数 <= 10000
1 <= value <= 10^5
当一个元素进入队列的时候,它前面所有比它小的元素就不会再对答案产生影响。所以我们只需要维护一个单调队列即可,在放入元素的时候,将单调队列里所有比该元素小的值poll,输出元素的时候,如果这个元素是当时的最大值,则将单调队列也进行poll。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class MaxQueue { private Queue<Integer> queue; private Deque<Integer> max; public MaxQueue () { queue=new LinkedList <>(); max=new LinkedList <>(); } public int max_value () { if (max.isEmpty())return -1 ; return max.getFirst(); } public void push_back (int value) { queue.add(value); while (!max.isEmpty()&&max.getLast()<value)max.pollLast(); max.add(value); } public int pop_front () { if (queue.isEmpty())return -1 ; int value=queue.poll(); if (max.getFirst()==value)max.pollFirst(); return value; } }
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
1 2 3 输入: coins = [1, 2, 5], amount = 11 输出: 3 解释: 11 = 5 + 5 + 1
示例 2:
1 2 输入: coins = [2], amount = 3 输出: -1
说明 :
动态规划,属于背包问题。dp[i][j]记录当只用前i种硬币组合j时的最少硬币个数,则有d p [ i ] [ j ] = min ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − c o i n s [ i ] ] + 1 ) dp[i][j]=\min(dp[i-1][j],dp[i][j-coins[i]]+1) d p [ i ] [ j ] = min ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − c o i n s [ i ] ] + 1 ) dp[i][j-coins[i]]存在的话。因为只使用了上一次的状态,所以可以用滚动数组进行优化。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public int coinChange (int [] coins, int amount) { int len=coins.length; int [] dp=new int [amount+1 ]; dp[0 ]=0 ; for (int i=1 ;i<amount+1 ;i++){ dp[i]=Integer.MAX_VALUE/2 ; } for (int i=0 ;i<len;i++){ for (int j=coins[i];j<amount+1 ;j++){ dp[j]=Integer.min(dp[j],dp[j-coins[i]]+1 ); } } if (dp[amount]>=amount+1 ){ return -1 ; } return dp[amount]; } }
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
注意:你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
示例 2:
输入: [7,6,4,3,1]
从前往后遍历,记录当前最小值与当前值减去最小值的差的最大值。
1 2 3 4 5 6 7 8 9 10 11 class Solution { public int maxProfit (int [] prices) { int res=0 ; int min=Integer.MAX_VALUE; for (int price : prices) { min=Math.min(min,price); res=Math.max(res,price-min); } return res; } }
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
1
/ \
2 3
/ \
4 5
返回 3 , 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
递归,其实最大直径就是左子树的深度+右子树的深度。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { private int res=0 ; public int diameterOfBinaryTree (TreeNode root) { deep(root); return res; } public int deep (TreeNode node) { if (node==null )return -1 ; int left=deep(node.left)+1 ; int right=deep(node.right)+1 ; res=Math.max(res,left+right); return Math.max(left,right); } }
给你一个整数数组 A,只有可以将其划分为三个和相等的非空部分时才返回 true,否则返回 false。
形式上,如果可以找出索引i+1 < j且满足 (A[0] + A[1] + ... + A[i] == A[i+1] + A[i+2] + ... + A[j-1] == A[j] + A[j-1] + ... + A[A.length - 1])就可以将数组三等分。
示例 1 :
1 2 3 输入:[0,2,1,-6,6,-7,9,1,2,0,1] 输出:true 解释:0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
示例 2:
1 2 输入:[0,2,1,-6,6,7,9,-1,2,0,1] 输出:false
示例 3 :
1 2 3 输入:[3,3,6,5,-2,2,5,1,-9,4] 输出:true 解释:3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4
先计算出总和,看能不能被3整除,然后模拟一下即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { public boolean canThreePartsEqualSum (int [] A) { int sum = 0 ; for (int num: A) { sum += num; } if (sum % 3 != 0 ) { return false ; } sum /= 3 ; int curSum = 0 , cnt = 0 ; for (int i = 0 ; i < A.length; i++) { curSum += A[i]; if (curSum == sum) { cnt++; curSum = 0 ; } } return cnt = = 3 || (cnt > 3 && sum == 0 ); } }
对于字符串 S 和 T,只有在 S = T + … + T(T 与自身连接 1 次或多次)时,我们才认定 “T 能除尽 S”。
返回最长字符串 X,要求满足 X 能除尽str1且 X 能除尽str2。
示例 1:
1 2 输入:str1 = "ABCABC", str2 = "ABC" 输出:"ABC"
示例 2:
1 2 输入:str1 = "ABABAB", str2 = "ABAB" 输出:"AB"
示例 3:
1 2 输入:str1 = "LEET", str2 = "CODE" 输出:""
提示:
1 <= str1.length <= 10001 <= str2.length <= 1000str1[i]和str2[i]为大写英文字母
如果两个字符串有公因子串,则必有str1+str2=str2+str1,用辗转相除法计算出长度的最大公因数,截取其中一段即为最大公因子串了。
1 2 3 4 5 6 7 8 9 class Solution { public String gcdOfStrings (String str1, String str2) { if (!(str1+str2).equals(str2+str1))return "" ; return str1.substring(0 ,gcd(str1.length(),str2.length())); } private int gcd (int a, int b) { return b==0 ?a:gcd(b,a%b); } }
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
示例 2:
1 2 输入: [2,2,1,1,1,2,2] 输出: 2
从第一个数开始count=1,遇到相同的就加1,遇到不同的就减1,减到0就重新换个数开始计数,因为最多的数出现的次数大于一半,所以最后总会找到这个数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { public int majorityElement (int [] nums) { int cur=nums[0 ]; int count=0 ; for (int num : nums) { if (num==cur)count++; else if (count==0 ){ cur=num; count=1 ; }else count--; } return cur; } }
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。O ( n 2 ) O(n^2) O ( n 2 )
常规dp就可以O ( n 2 ) O(n^2) O ( n 2 )
考虑一个简单的贪心,如果我们要使上升子序列尽可能的长,则我们需要让序列上升得尽可能慢,因此我们希望每次在上升子序列最后加上的那个数尽可能的小。
基于上面的贪心思路,我们维护一个数组 d[i] ,表示长度为 ii 的最长上升子序列的末尾元素的最小值,用 l e n len l e n l e n len l e n d [ 1 ] = n u m s [ 0 ] d[1]=nums[0] d [ 1 ] = n u m s [ 0 ]
同时我们可以注意到 d[i]d[i] 是关于 ii 单调递增的。因为如果 d [ j ] ≥ d [ i ] d[j] \geq d[i] d [ j ] ≥ d [ i ] i − j i-j i − j
我们依次遍历数组 $nums[] $中的每个元素,并更新数组 d[]d[] 和 l e n len l e n l e n = l e n + 1 len = len + 1 l e n = l e n + 1 d [ 1 … l e n ] d[1 \ldots len] d [ 1 … l e n ] d [ i ] = n u m s [ j ] d[i]=nums[j] d [ i ] = n u m s [ j ]
根据 d 数组的单调性,我们可以使用二分查找寻找下标 i,优化时间复杂度。
最后整个算法流程为:
设当前已求出的最长上升子序列的长度为$ len$(初始时为 11),从前往后遍历数组 n u m s nums n u m s
如果$nums[i]>d[len] $,则直接加入到 d 数组末尾,并更新 l e n = l e n + 1 len=len+1 l e n = l e n + 1
否则,在 d 数组中二分查找,找到第一个比$nums[i] $小的数 d[k] ,并更新 d [ k + 1 ] = n u m s [ i ] d[k+1]=nums[i] d [ k + 1 ] = n u m s [ i ]
作者:LeetCode-Solutionhttps://leetcode-cn.com/problems/longest-increasing-subsequence/solution/zui-chang-shang-sheng-zi-xu-lie-by-leetcode-soluti/
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution { public int lengthOfLIS (int [] nums) { int len = 1 , n = (int )nums.length; if (n == 0 ) return 0 ; int [] d=new int [n+1 ]; d[len] = nums[0 ]; for (int i = 1 ; i < n; ++i) { if (nums[i] > d[len]) d[++len] = nums[i]; else { int l = 1 , r = len, pos = 0 ; while (l <= r) { int mid = (l + r) >> 1 ; if (d[mid] < nums[i]) { pos = mid; l = mid + 1 ; } else r = mid - 1 ; } d[pos + 1 ] = nums[i]; } } return len; } }
给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
示例 1:
1 2 3 4 5 6 7 8 [[0,0,1,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,1,1,0,1,0,0,0,0,0,0,0,0], [0,1,0,0,1,1,0,0,1,0,1,0,0], [0,1,0,0,1,1,0,0,1,1,1,0,0], [0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,0,0,0,0,0,0,1,1,0,0,0,0]]
对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ,因为岛屿只能包含水平或垂直的四个方向的 1 。
示例 2:
对于上面这个给定的矩阵, 返回 0。
对于每个1进行dfs。下面的代码其实可以不必使用cur标记是否访问,直接对访问过进行置0即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution { private int [][]conditions={{-1 ,0 },{1 ,0 },{0 ,-1 },{0 ,1 }}; private boolean [][] cur; private int res=0 ; public int maxAreaOfIsland (int [][] grid) { if (grid.length==0 ||grid[0 ].length==0 )return 0 ; cur=new boolean [grid.length][grid[0 ].length]; int cur_res=0 ; for (int i = 0 ; i < grid.length; i++) { for (int j = 0 ; j < grid[0 ].length; j++) { if (grid[i][j]==1 &&!cur[i][j]){ cur_res=maxAreaOfIsland(grid,i,j); res=Math.max(res,cur_res); } } } return res; } public int maxAreaOfIsland (int [][] grid,int i,int j) { int cur_res=0 ; if (i<0 ||i==grid.length||j<0 ||j==grid[0 ].length||cur[i][j]||grid[i][j]!=1 )return cur_res; cur_res++; cur[i][j]=true ; for (int k = 0 ; k < 4 ; k++) { cur_res+=maxAreaOfIsland(grid,i+conditions[k][0 ],j+conditions[k][1 ]); } return cur_res; } }
字符串压缩。利用字符重复出现的次数,编写一种方法,实现基本的字符串压缩功能。比如,字符串aabcccccaaa会变为a2b1c5a3。若“压缩”后的字符串没有变短,则返回原先的字符串。你可以假设字符串中只包含大小写英文字母(a至z)。
示例1:
1 2 输入:"aabcccccaaa" 输出:"a2b1c5a3"
示例2:
1 2 3 输入:"abbccd" 输出:"abbccd" 解释:"abbccd"压缩后为"a1b2c2d1",比原字符串长度更长。
提示:
直接模拟这个过程即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution { public String compressString (String S) { if (S.length()<3 )return S; StringBuilder sb=new StringBuilder (); char c=S.charAt(0 ); int count=1 ; for (int i = 1 ; i < S.length(); i++) { if (S.charAt(i)==c){ count++; }else { sb.append(c).append(count); if (sb.length()>=S.length()){ return S; } c=S.charAt(i); count=1 ; } } sb.append(c).append(count); if (sb.length()>=S.length()){ return S; } return sb.toString(); } }
给你一份『词汇表』(字符串数组) words 和一张『字母表』(字符串) chars。
假如你可以用 chars 中的『字母』(字符)拼写出 words 中的某个『单词』(字符串),那么我们就认为你掌握了这个单词。
注意:每次拼写(指拼写词汇表中的一个单词)时,chars 中的每个字母都只能用一次。
返回词汇表 words 中你掌握的所有单词的 长度之和。
示例 1:
1 2 3 4 输入:words = ["cat","bt","hat","tree"], chars = "atach" 输出:6 解释: 可以形成字符串 "cat" 和 "hat",所以答案是 3 + 3 = 6。
示例 2:
1 2 3 4 输入:words = ["hello","world","leetcode"], chars = "welldonehoneyr" 输出:10 解释: 可以形成字符串 "hello" 和 "world",所以答案是 5 + 5 = 10。
提示:
1 <= words.length <= 10001 <= words[i].length, chars.length <= 100所有字符串中都仅包含小写英文字母
只有26个字母,直接数组哈希。逐个测试即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public int countCharacters (String[] words, String chars) { int [] hash = new int [26 ]; for (char ch : chars.toCharArray()){ hash[ch - 'a' ] += 1 ; } int [] map = new int [26 ]; int len = 0 ; for (String word : words){ Arrays.fill(map, 0 ); boolean flag = true ; for (char ch : word.toCharArray()){ map[ch - 'a' ]++; if (map[ch - 'a' ] > hash[ch - 'a' ]) flag = false ; } len += flag ? word.length() : 0 ; } return len; } }
矩形以列表 [x1, y1, x2, y2] 的形式表示,其中 (x1, y1) 为左下角的坐标,(x2, y2) 是右上角的坐标。
如果相交的面积为正,则称两矩形重叠。需要明确的是,只在角或边接触的两个矩形不构成重叠。
给出两个矩形,判断它们是否重叠并返回结果。
示例 1:
1 2 输入:rec1 = [0,0,2,2], rec2 = [1,1,3,3] 输出:true
示例 2:
1 2 输入:rec1 = [0,0,1,1], rec2 = [1,0,2,1] 输出:false
提示:
两个矩形 rec1 和 rec2 都以含有四个整数的列表的形式给出。
矩形中的所有坐标都处于 -10^9 和 10^9 之间。
x 轴默认指向右,y 轴默认指向上。
你可以仅考虑矩形是正放的情况。
矩形如果不重叠,从x轴和y轴上看两个矩形就变成了两条线段,这两条线段肯定是不相交的,也就是说左边的矩形的最右边小于右边矩形的最左边,也就是rec1[2] < rec2[0] || rec2[2] < rec1[0];y轴同理,下面的矩形的最上边小于上面矩形的最下边,也就是rec1[3] < rec2[1] || rec2[3] < rec1[1]。因为题目要求重叠算相离,所以加上=,最后取反就行啦~
1 2 3 4 5 class Solution { public boolean isRectangleOverlap (int [] rec1, int [] rec2) { return !(rec1[0 ] >= rec2[2 ] || rec1[2 ] <= rec2[0 ] || rec1[1 ] >= rec2[3 ] || rec1[3 ] <= rec2[1 ]); } }
给定一个包含大写字母和小写字母的字符串,找到通过这些字母构造成的最长的回文串。
在构造过程中,请注意区分大小写。比如 "Aa" 不能当做一个回文字符串。
注意:
示例 1:
1 2 3 4 5 6 7 8 输入: "abccccdd" 输出: 7 解释: 我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。
直接统计每个字符的个数。只要是复数出现的即可,最后还可以加上一个正中间的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public int longestPalindrome (String s) { int [] cnts = new int [58 ]; for (int i = 0 ; i < s.length(); i++) { cnts[s.charAt(i) - 'A' ]++; } int palindrome = 0 ; for (int cnt : cnts) { palindrome += (cnt / 2 ) * 2 ; } if (palindrome < s.length()) { palindrome++; } return palindrome; } }
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
1 2 输入:arr = [3,2,1], k = 2 输出:[1,2] 或者 [2,1]
示例 2:
1 2 输入:arr = [0,1,2,1], k = 1 输出:[0]
限制:
0 <= k <= arr.length <= 100000 <= arr[i] <= 10000
二分法,每次取mid,将数组分为两个部分,如果小的那部分>k,则继续再这部分进行二分,如果<k,则这些数都是结果,再在大的部分继续取剩下的数,如果刚好等于要取的数,则结束。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution { public int [] getLeastNumbers(int [] arr, int k) { int [] res=new int [k]; int len=arr.length; int leftL,rightL; int [] left=new int [len]; int [] right=new int [len]; int index=0 ; int mid; int [] midA=new int [len]; int midL; while (index<k){ leftL=0 ;rightL=0 ;midL=0 ; mid=arr[len/2 ]; for (int i = 0 ; i < len; i++) { if (arr[i]<mid){ left[leftL++]=arr[i]; }else if (arr[i]==mid)midA[midL++]=arr[i]; else right[rightL++]=arr[i]; } if (leftL>(k-index)){ arr=left; len=leftL; }else { for (int i = 0 ; i < leftL; i++) { res[index++]=left[i]; } int tmp=0 ; while (index<k&&tmp<midL){ res[index++]=midA[tmp++]; } arr=right; len=rightL; } } return res; } }
有两个容量分别为 x升 和 y升 的水壶以及无限多的水。请判断能否通过使用这两个水壶,从而可以得到恰好 z升 的水?
如果可以,最后请用以上水壶中的一或两个来盛放取得的 z升 水。
你允许:
装满任意一个水壶
清空任意一个水壶
从一个水壶向另外一个水壶倒水,直到装满或者倒空
示例 1: (From the famous “Die Hard” example
1 2 输入: x = 3, y = 5, z = 4 输出: True
示例 2:
1 2 输入: x = 2, y = 6, z = 5 输出: False
预备知识:贝祖定理
我们认为,每次操作只会让桶里的水总量增加 x,增加 y,减少 x,或者减少 y。
你可能认为这有问题:如果往一个不满的桶里放水,或者把它排空呢?那变化量不就不是 x 或者 y 了吗?接下来我们来解释这一点:
首先要清楚,在题目所给的操作下,两个桶不可能同时有水且不满。因为观察所有题目中的操作,操作的结果都至少有一个桶是空的或者满的;
其次,对一个不满的桶加水是没有意义的。因为如果另一个桶是空的,那么这个操作的结果等价于直接从初始状态给这个桶加满水;而如果另一个桶是满的,那么这个操作的结果等价于从初始状态分别给两个桶加满;
再次,把一个不满的桶里面的水倒掉是没有意义的。因为如果另一个桶是空的,那么这个操作的结果等价于回到初始状态;而如果另一个桶是满的,那么这个操作的结果等价于从初始状态直接给另一个桶倒满。
因此,我们可以认为每次操作只会给水的总量带来 x 或者 y 的变化量。因此我们的目标可以改写成:找到一对整数 a,b,使得
a x + b y = z ax+by=z
a x + b y = z
而只要满足z≤x+y,且这样的 a,b 存在,那么我们的目标就是可以达成的。这是因为:
而贝祖定理告诉我们,ax+by=z 有解当且仅当 z 是 x,y 的最大公约数的倍数。因此我们只需要找到x,y 的最大公约数并判断 z 是否是它的倍数即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution { public boolean canMeasureWater (int x, int y, int z) { if (x+y<z)return false ; if (x+y==z||x==z||y==z||x==1 ||y==1 )return true ; if (x==y||x==0 ||y==0 )return false ; if (z==0 )return true ; int gcd=getGCD(x,y); if (gcd==1 )return true ; return gcd<z&&z%gcd==0 ; } private int getGCD (int a, int b) { if (a < 0 || b < 0 ) { return -1 ; } if (b == 0 ) { return a; } while (a % b != 0 ) { int temp = a % b; a = b; b = temp; } return b; } }
给定整数数组 A,每次 move 操作将会选择任意 A[i],并将其递增 1。
返回使 A 中的每个值都是唯一的最少操作次数。
示例 1:
1 2 3 输入:[1,2,2] 输出:1 解释:经过一次 move 操作,数组将变为 [1, 2, 3]。
示例 2:
1 2 3 4 输入:[3,2,1,2,1,7] 输出:6 解释:经过 6 次 move 操作,数组将变为 [3, 4, 1, 2, 5, 7]。 可以看出 5 次或 5 次以下的 move 操作是不能让数组的每个值唯一的。
提示:
0 <= A.length <= 400000 <= A[i] < 40000
首先模拟也可以做,但是很慢,所以可以利用空间换时间的方法,记录下所有的数出现的次数,遍历这些数,对于每个数出现次数>1的数进行次数-1的move操作,所以该数+1要的次数要加上该数的次数-1,结果加上move的次数即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { public int minIncrementForUnique (int [] A) { int [] arr=new int [50000 ]; int res=0 ; for (int i:A){ arr[i]++; } for (int i = 0 ; i < 50000 ; i++) { if (arr[i]>1 ){ arr[i+1 ]+=arr[i]-1 ; res+=arr[i]-1 ; } } return res; } }
给定一个带有头结点 head 的非空单链表,返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
示例 1:
1 2 3 4 5 输入:[1,2,3,4,5] 输出:此列表中的结点 3 (序列化形式:[3,4,5]) 返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。 注意,我们返回了一个 ListNode 类型的对象 ans,这样: ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
示例 2:
1 2 3 输入:[1,2,3,4,5,6] 输出:此列表中的结点 4 (序列化形式:[4,5,6]) 由于该列表有两个中间结点,值分别为 3 和 4,我们返回第二个结点。
提示:
经典的快慢指针用法。
1 2 3 4 5 6 7 8 9 10 11 class Solution { public ListNode middleNode (ListNode head) { ListNode low = head, fast = head; while (fast != null && fast.next != null ) { fast = fast.next.next; low = low.next; } return low; } }
一个有名的按摩师会收到源源不断的预约请求,每个预约都可以选择接或不接。在每次预约服务之间要有休息时间,因此她不能接受相邻的预约。给定一个预约请求序列,替按摩师找到最优的预约集合(总预约时间最长),返回总的分钟数。
注意:本题相对原题稍作改动
示例 1:
1 2 3 输入: [1,2,3,1] 输出: 4 解释: 选择 1 号预约和 3 号预约,总时长 = 1 + 3 = 4。
示例 2:
1 2 3 输入: [2,7,9,3,1] 输出: 12 解释: 选择 1 号预约、 3 号预约和 5 号预约,总时长 = 2 + 9 + 1 = 12。
示例 3:
1 2 3 输入: [2,1,4,5,3,1,1,3] 输出: 12 解释: 选择 1 号预约、 3 号预约、 5 号预约和 8 号预约,总时长 = 2 + 4 + 3 + 3 = 12。
动态规划:d p [ i ] = max ( d p [ i − 1 ] , d p [ i − 2 ] + n u m s [ i ] ) dp[i]=\max(dp[i-1],dp[i-2]+nums[i]) d p [ i ] = max ( d p [ i − 1 ] , d p [ i − 2 ] + n u m s [ i ] )
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public int massage (int [] nums) { if (nums.length==0 )return 0 ; if (nums.length==1 )return nums[0 ]; int [] dp=new int [nums.length]; dp[0 ]=nums[0 ]; dp[1 ]= Math.max(nums[1 ], nums[0 ]); for (int i = 2 ; i < nums.length; i++) { dp[i]=Math.max(dp[i-1 ],dp[i-2 ]+nums[i]); } return dp[nums.length-1 ]; } }
在 N * N 的网格上,我们放置一些 1 * 1 * 1 的立方体。
每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。
请你返回最终形体的表面积。
示例 1:
示例 2:
示例 3:
示例 4:
1 2 输入:[[1,1,1],[1,0,1],[1,1,1]] 输出:32
示例 5:
1 2 输入:[[2,2,2],[2,1,2],[2,2,2]] 输出:46
提示:
1 <= N <= 500 <= grid[i][j] <= 50
对于每个格子里的正方体,首先是上下两个面,然后是每个有四个侧面,最后减去重复计算的侧面即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public int surfaceArea (int [][] grid) { if (grid.length==0 ||grid[0 ].length==0 )return 0 ; int res=0 ; for (int i = 0 ; i < grid.length; i++) { for (int j = 0 ; j < grid[0 ].length; j++) { if (grid[i][j]!=0 ){ res+=2 ; res+=grid[i][j]<<2 ; if (i>0 )res-=Math.min(grid[i][j],grid[i-1 ][j])<<1 ; if (j>0 )res-=Math.min(grid[i][j],grid[i][j-1 ])<<1 ; } } } return res; } }
在一个 8 x 8 的棋盘上,有一个白色的车(Rook),用字符 'R' 表示。棋盘上还可能存在空方块,白色的象(Bishop)以及黑色的卒(pawn),分别用字符 '.','B' 和 'p' 表示。不难看出,大写字符表示的是白棋,小写字符表示的是黑棋。
车按国际象棋中的规则移动。东,西,南,北四个基本方向任选其一,然后一直向选定的方向移动,直到满足下列四个条件之一:
棋手选择主动停下来。
棋子因到达棋盘的边缘而停下。
棋子移动到某一方格来捕获位于该方格上敌方(黑色)的卒,停在该方格内。
车不能进入/越过已经放有其他友方棋子(白色的象)的方格,停在友方棋子前。
你现在可以控制车移动一次,请你统计有多少敌方的卒处于你的捕获范围内(即,可以被一步捕获的棋子数)。
示例 1:
1 2 3 4 5 6 7 8 9 10 11 12 输入: [[".",".",".",".",".",".",".","."], [".",".",".","p",".",".",".","."], [".",".",".","R",".",".",".","p"], [".",".",".",".",".",".",".","."], [".",".",".",".",".",".",".","."], [".",".",".","p",".",".",".","."], [".",".",".",".",".",".",".","."], [".",".",".",".",".",".",".","."]] 输出:3 解释: 在本例中,车能够捕获所有的卒。
提示:
board.length == board[i].length == 8board[i][j]可以是'R','.','B'或 'p'只有一个格子上存在board[i][j] == 'R'
很没意思的一道题。。。。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Solution { public int numRookCaptures (char [][] board) { int res=0 ; int row=0 ,col=0 ; for (int i = 0 ; i < board.length; i++) { for (int j = 0 ; j < board[i].length; j++) { if (board[i][j]=='R' ){ row=i;col=j;break ; } } } int tmp=row-1 ; while (tmp>=0 ){ char c=board[tmp][col]; if (c=='B' )break ; if (c=='p' ){res++;break ;} tmp--; } tmp=row+1 ; while (tmp<board.length){ char c=board[tmp][col]; if (c=='B' )break ; if (c=='p' ){res++;break ;} tmp++; } tmp=col-1 ; while (tmp>=0 ){ char c=board[row][tmp]; if (c=='B' )break ; if (c=='p' ){res++;break ;} tmp--; } tmp=col+1 ; while (tmp<board[0 ].length){ char c=board[row][tmp]; if (c=='B' )break ; if (c=='p' ){res++;break ;} tmp++; } return res; } }
给定一副牌,每张牌上都写着一个整数。
此时,你需要选定一个数字 X,使我们可以将整副牌按下述规则分成 1 组或更多组:
每组都有 X 张牌。
组内所有的牌上都写着相同的整数。
仅当你可选的 X >= 2 时返回 true。
示例 1:
1 2 3 输入:[1,2,3,4,4,3,2,1] 输出:true 解释:可行的分组是 [1,1],[2,2],[3,3],[4,4]
示例 2:
1 2 3 输入:[1,1,1,2,2,2,3,3] 输出:false 解释:没有满足要求的分组。
示例 3:
1 2 3 输入:[1] 输出:false 解释:没有满足要求的分组。
示例 4:
1 2 3 输入:[1,1] 输出:true 解释:可行的分组是 [1,1]
示例 5:
1 2 3 输入:[1,1,2,2,2,2] 输出:true 解释:可行的分组是 [1,1],[2,2],[2,2]
提示:
1 <= deck.length <= 100000 <= deck[i] < 10000
先给这些牌排个序。
然后记录所有牌的张数。以及最少的张数。
然后从2…最少的张数进行测试可否分组。
下面的代码写成hash会更好一点,懒得写了。。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { public boolean hasGroupsSizeX (int [] deck) { Arrays.sort(deck); List<Integer> list=new ArrayList <>(); int min=Integer.MAX_VALUE; int tmp=1 ; for (int i = 1 ; i < deck.length; i++) { if (deck[i]==deck[i-1 ])tmp++; else { if (tmp==1 )return false ; min=Math.min(min,tmp); list.add(tmp); tmp=1 ; } } if (tmp==1 )return false ; min=Math.min(min,tmp); list.add(tmp); tmp=min; boolean flag=true ; for (int i = 2 ; i <= min; i++) { flag=true ; if (min%i==0 ){ for (Integer ii:list){ if (ii % i != 0 ) { flag = false ; break ; } } if (flag)return true ; } } return false ; } }
给定一个单词列表,我们将这个列表编码成一个索引字符串 S 与一个索引列表 A。
例如,如果这个列表是 ["time", "me", "bell"],我们就可以将其表示为 S = "time#bell#" 和 indexes = [0, 2, 5]。
对于每一个索引,我们可以通过从字符串 S 中索引的位置开始读取字符串,直到 “#” 结束,来恢复我们之前的单词列表。
那么成功对给定单词列表进行编码的最小字符串长度是多少呢?
示例:
1 2 3 输入: words = ["time", "me", "bell"] 输出: 10 说明: S = "time#bell#" , indexes = [0, 2, 5] 。
提示:
1 <= words.length <= 20001 <= words[i].length <= 7每个单词都是小写字母 。
很烂的思路,先对单词进行按长度排序。然后遍历判断是否以其他单词结尾的,如果有单词被别的单词包含就不计算,最后的结果就是没有被包含的单词的长度+1的和。
最好的做法是用字典树(前缀树),奈何不会~待学。。
这道题将字符串倒过来就是判断前缀是否包含单词了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public int minimumLengthEncoding (String[] words) { Arrays.sort(words,(a,b)->(Integer.compare(b.length(), a.length()))); boolean [] flags=new boolean [words.length]; for (int i = 0 ; i < words.length; i++) { String tmp=words[i]; for (int j = i+1 ; j < words.length; j++) { if (!flags[j]&&tmp.endsWith(words[j])){ flags[j]=true ; } } } int res=0 ; for (int i = 0 ; i < words.length; i++) { if (!flags[i])res+=words[i].length()+1 ; } return res; } }
字典树做法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class Solution { public int minimumLengthEncoding (String[] words) { int len = 0 ; Trie trie = new Trie (); Arrays.sort(words, (s1, s2) -> s2.length() - s1.length()); for (String word: words) { len += trie.insert(word); } return len; } } class Trie { TrieNode root; public Trie () { root = new TrieNode (); } public int insert (String word) { TrieNode cur = root; boolean isNew = false ; for (int i = word.length() - 1 ; i >= 0 ; i--) { int c = word.charAt(i) - 'a' ; if (cur.children[c] == null ) { isNew = true ; cur.children[c] = new TrieNode (); } cur = cur.children[c]; } return isNew? word.length() + 1 : 0 ; } } class TrieNode { char val; TrieNode[] children = new TrieNode [26 ]; public TrieNode () {} }
你现在手里有一份大小为 N x N 的「地图」(网格) grid,上面的每个「区域」(单元格)都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,请你找出一个海洋区域,这个海洋区域到离它最近的陆地区域的距离是最大的。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。
如果我们的地图上只有陆地或者海洋,请返回 -1。
示例 1:
1 2 3 4 输入:[[1,0,1],[0,0,0],[1,0,1]] 输出:2 解释: 海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大,最大距离为 2。
示例 2:
1 2 3 4 输入:[[1,0,0],[0,0,0],[0,0,0]] 输出:4 解释: 海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大,最大距离为 4。
提示:
1 <= grid.length == grid[0].length <= 100grid[i][j] 不是 0 就是 1
先找出所有的陆地,再从陆地开始进行分层的BFS,遍历的最大深度即为解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { private int [][]conditions={{-1 ,0 },{1 ,0 },{0 ,-1 },{0 ,1 }}; public int maxDistance (int [][] grid) { int N=grid.length; Queue<int []> queue=new LinkedList <>(); for (int i = 0 ; i < N; i++) { for (int j = 0 ; j < N; j++) { if (grid[i][j]==1 ){ queue.add(new int []{i,j}); } } } if (queue.size()==N*N||queue.size()==0 )return -1 ; int res=-1 ; while (!queue.isEmpty()){ res++; int tmp=queue.size(); for (int k = 0 ; k < tmp; k++) { int [] poi=queue.poll(); int i=poi[0 ],j=poi[1 ]; for (int l = 0 ; l < 4 ; l++) { int newi=i+conditions[l][0 ]; int newj=j+conditions[l][1 ]; if (newi<0 ||newj<0 ||newi==N||newj==N)continue ; if (grid[newi][newj]==0 ){ grid[newi][newj]=-1 ; queue.add(new int []{newi,newj}); } } } } return res; } }
0,1,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
示例 1:
示例 2:
1 2 输入: n = 10, m = 17 输出: 2
限制:
1 <= n <= 10^51 <= m <= 10^6
首先是模拟这个过程,但是会超时,官方给出数学法 :
【思路】
n个数字的圆圈,不断删除第m个数字,我们把最后剩下的数字记为f(n,m)
原始数组
映射数字
k+1
0
k+2
1
…
…
n-1
n-k-2
0
n-k-1
…
…
k-1
n-2
把映射数字记为x,原始数字记为y,那么映射数字变回原始数字的公式为
y = ( x + k + 1 ) m o d n y=(x+k+1)\mod n
y = ( x + k + 1 ) m o d n
在映射数字中,n-1个数字,不断删除第m个数字,由定义可以知道,最后剩下的数字为f(n-1,m)。我们把它变回原始数字,由上一个公式可以得到最后剩下的原始数字是(f(n-1,m)+k+1)%n,而这个数字也就是一开始我们标记的f(n,m),所以可以推得递归公式为
f ( n , m ) = ( f ( n − 1 , m ) + k + 1 ) m o d n f(n,m) =(f(n-1,m)+k+1)\mod n
f ( n , m ) = ( f ( n − 1 , m ) + k + 1 ) m o d n
将k=(m-1)%n代入,化简得到:
f ( n , m ) = ( f ( n − 1 , m ) + m ) m o d n , 且 f ( 1 , m ) = 0 f(n,m) =(f(n-1,m)+m)\mod n, 且f(1,m) = 0
f ( n , m ) = ( f ( n − 1 , m ) + m ) m o d n , 且 f ( 1 , m ) = 0
代码中可以采用迭代或者递归的方法实现该递归公式。时间复杂度为O(n),空间复杂度为O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution { public int lastRemaining (int n, int m) { int res = 0 ; for (int i = 2 ; i <= n; i++) { res = (res + m) % i; } return res; } }
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
1 2 输入:nums = [5,2,3,1] 输出:[1,2,3,5]
示例 2:
1 2 输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 50000-50000 <= nums[i] <= 50000
各种排序~
1 2 3 4 5 6 class Solution { public int [] sortArray(int [] nums) { Arrays.sort(nums); return nums; } }